introducción.
circunferencia.
La circunferencia es una curva plana y cerrada donde todos sus puntos están a igual distancia del centro.
La circunferencia solo posee longitud. Se distingue del círculo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia es el perímetro del círculo cuya superficie contiene.
Puede ser considerada como una elipse de excentricidad nula, o una elipse cuyos semiejes son iguales, o los focos coinciden. También se puede describir como la sección, perpendicular al eje, de una superficie cónica o cilíndrica, o como unpolígono regular de infinitos lados, cuya apotema coincide con su radio.
La intersección de un plano con una superficie esférica puede ser: o bien el conjunto vacío (plano exterior); o bien un solo punto (plano tangente); o bien una circunferencia, si el plano secante pasa por el centro , se llama ecuador
La circunferencia de centro en el origen de coordenadas y radio 1 se denomina circunferencia unidad o circunferencia goniométrica.
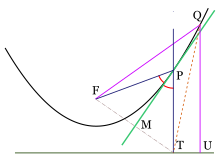
En matemáticas, una parábola (del griego παραβολή) es la sección cónica resultante de cortar un cono recto con un plano cuyo ángulo de inclinación respecto al eje de revolución del cono sea igual al presentado por su generatriz. El plano resultará por lo tanto paralelo a dicha recta. Se define también como el lugar geométrico de los puntos de un plano que equidistan de una recta llamadadirectriz, y un punto exterior a ella llamado foco. En geometría proyectiva, la parábola se define como la curva envolvente de las rectas que unen pares de puntos homólogos en una proyectividadsemejante o semejanza.
La parábola aparece en muchas ramas de las ciencias aplicadas debido a que su forma se corresponde con las gráficas de las ecuaciones cuadráticas. Por ejemplo, son parábolas las trayectorias ideales de los cuerpos que se mueven bajo la influencia exclusiva de la gravedad (ver movimiento parabólico y trayectoria balística).

La elipse es el lugar geométrico de todos los puntos de un plano, tales que la suma de las distancias a otros dos puntos fijos llamados focos es constante.








 de una circunferencia es:
de una circunferencia es: es la longitud del radio.
es la longitud del radio. (
(
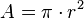
 .
.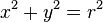 .
.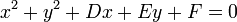



 ,
,





 . La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.
. La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.