Circunferencia.La circunferencia es una curva plana y cerrada donde todos sus puntos están a igual distancia del centro.z
La circunferencia solo posee longitud. Se distingue del círculo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia es el perímetro del círculo cuya superficie contiene.Puede ser considerada como una elipse de excentricidad nula, o una elipse cuyos semiejes son iguales, o los focos coinciden. También se puede describir como la sección, perpendicular al eje, de una superficie cónica o cilíndrica, o como unpolígono regular de infinitos lados, cuya apotema coincide con su radio.La intersección de un plano con una superficie esférica puede ser: o bien el conjunto vacío (plano exterior); o bien un solo punto (plano tangente); o bien una circunferencia, si el plano secante pasa por el centro , se llama ecuadorLa circunferencia de centro en el origen de coordenadas y radio 1 se denomina circunferencia unidad o circunferencia goniométrica. Elementos de la circunferenciaExisten varios puntos, rectas y segmentos, singulares en la circunferencia:
Elementos de la circunferenciaExisten varios puntos, rectas y segmentos, singulares en la circunferencia:
- Centro, el punto interior equidistante de todos los puntos de la circunferencia;
- Radio, El radio de una circunferencia es el segmento que une el centro de la circunferencia con un punto cualquiera de la misma. El radio mide la mitad del diámetro.El radio es igual a la longitud de la circunferencia dividida entre 2π.
- Diámetro, El diámetro de una circunferencia es el segmento que une dos puntos de la circunferencia y pasa por el centro. El diámetro mide el doble del radio. El diámetro es igual a la longitud de la circunferencia dividida entre π;
- Cuerda, La cuerda es un segmento que une dos puntos de la circunferencia. El diámetro es la cuerda de longitud máxima.
- Recta secante, Es la línea que corta a la circunferencia en dos puntos;
- Recta tangente, Es la línea que toca a la circunferencia en un sólo punto;
- Punto de Tangencia, el de contacto de la recta tangente con la circunferencia;
- Arco, El arco de la circunferencia es cada una de las partes en que una cuerda divide a la circunferencia. Un arco de circunferencia se denota con el símbolo sobre las letras de los puntos extremos del arco.
- Semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diámetro.

Diámetros conjugados.Dos diámetros de una sección cónica se denominan conjugados cuando toda cuerda paralela a uno de ellos es bisecada por el otro. Por ejemplo, dos diámetros de la circunferencia perpendiculares entre sí son mutuamente conjugados. En una elipse dos diámetros son conjugados si y sólo si la tangente a la elipse en el extremo de un diámetro es paralela a la tangente al segundo extremo. Punto interior.Es un punto en el plano de la circunferencia, cuya distancia al centro de la circunferencia es menor que el radio. El conjunto de todos los puntos interiores se llama interior de la circunferencia. Respecto al círculo, nítidamente, se distinguen el interior, el exterior y la frontera, que es precisamente la respectiva circunferencia.La circunferencia y un punto.
Punto interior.Es un punto en el plano de la circunferencia, cuya distancia al centro de la circunferencia es menor que el radio. El conjunto de todos los puntos interiores se llama interior de la circunferencia. Respecto al círculo, nítidamente, se distinguen el interior, el exterior y la frontera, que es precisamente la respectiva circunferencia.La circunferencia y un punto.
- Exterior a la circunferencia, si la distancia del centro al punto es mayor que la longitud del radio.
- Perteneciente a la circunferencia, si la distancia del centro al punto es igual a la longitud del radio.
- Interior a la circunferencia, si la distancia del centro al punto es menor a la longitud del radio.
 La circunferencia y la recta.
La circunferencia y la recta.
- Exterior, si no tienen ningún punto en común con ella y la distancia del centro a la recta es mayor que la longitud del radio.
- Tangente, si la toca en un punto (el punto de tangencia o tangente) y la distancia del centro a la recta es igual a la longitud del radio. Una recta tangente a una circunferencia es perpendicular al radio que une el punto de tangencia con el centro.
- Secante, si tiene dos puntos comunes, es decir, si la corta en dos puntos distintos y la distancia del centro a la recta es menor a la longitud del radio.
- Segmento circular, es el conjunto de puntos de la región circular comprendida entre una cuerda y el arco correspondiente.
Dos circunferencias.
- Exteriores, si no tienen puntos comunes y la distancia que hay entre sus centros es mayor que la suma de sus radios. No importa que tengan igual o distinto radio. (Figura 1)
- Tangentes exteriormente, si tienen un punto común y todos los demás puntos de una son exteriores a la otra. La distancia que hay entre sus centros es igual a la suma de sus radios. No importa que tengan igual o distinto radio. (Figura 2)
- Secantes, si se cortan en dos puntos distintos y la distancia entre sus centros es menor a la suma de sus radios. No importa que tengan igual o distinto radio. Dos circunferencias distintas no pueden cortarse en más de dos puntos. Dos circunferencias son secantes ortogonalmente si el ángulo entre sus tangentes en los dos puntos de contacto es recto. (Figura 3)
- Tangentes interiormente, si tienen un punto común y todos los demás puntos de una de ellas son interiores a la otra exclusivamente. La distancia que hay entre sus centros es igual al valor absoluto de la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra. (Figura 4)
- Interiores excéntricas, si no tienen ningún punto común y la distancia entre sus centros es mayor que 0 y menor que el valor absoluto de la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra.
- Interiores concéntricas, si tienen el mismo centro (la distancia entre sus centros es 0) y distinto radio. Forman una figura conocida como corona circular o anillo. Una de ellas tiene que tener mayor radio que la otra. (Figura 5)
- Coincidentes, si tienen el mismo centro y el mismo radio. Si dos circunferencias tienen más de dos puntos comunes, necesariamente son circunferencias coincidentes.
Un punto en el plano puede ser:Una recta, respecto de una circunferencia, puede ser:Dos circunferencias, en función de sus posiciones relativas, se denominan:
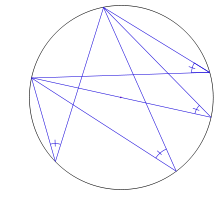
Ángulos en una circunferencia.La amplitud de un ángulo central es igual a la del arco que abarca.La amplitud de un ángulo inscrito en una semi circunferencia equivale a la mayor parte del ángulo exterior que limita dicha base. (Véase: arco capaz.)La amplitud de un ángulo semi-inscrito es la mitad de la del arco que abarca.La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones.Un ángulo, respecto de una circunferencia, pueden ser:Ángulo central, si tiene su vértice en el centro de esta. Sus lados contienen a dos radios.
Ángulo inscrito, si su vértice es un punto de la circunferencia y sus lados contienen dos cuerdas.
Ángulo semi-inscrito, si su vértice es un punto de la circunferencia y sus lados contienen una cuerda y una recta tangente a la circunferencia. El vértice es el punto de tangencia.
Ángulo interior, si su vértice está en el interior de la circunferencia.
Ángulo exterior, si tiene su vértice en el exterior de la circunferencia.

Longitud de la circunferencia. La longitud
La longitud 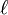 de una circunferencia es:donde
de una circunferencia es:donde  es la longitud del radio.
es la longitud del radio.
Pues 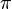 (número pi), por definición, es el cociente entre la longitud de la circunferencia y el diámetro:
(número pi), por definición, es el cociente entre la longitud de la circunferencia y el diámetro:

Área del círculo delimitado por una circunferencia.El área del círculo delimitado por la circunferencia es: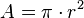
Ecuaciones de la circunferencia. .
.
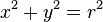 .
.

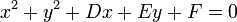



En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (a, b) y radio r consta de todos los puntos (x, y) que satisfacen la ecuaciónCuando el centro está en el origen (0, 0), la ecuación anterior se simplifica al
La circunferencia con centro en el origen y de radio la unidad, es llamada circunferencia goniométrica, circunferencia unidad o circunferencia unitaria.
De la ecuación general de una circunferencia,
se deduce:
resultando:
Si conocemos los puntos extremos de un diámetro:  ,
,
la ecuación de la circunferencia es:


Parábola.Propiedades geométricasAunque la definición original de la parábola es la relativa a la sección de un cono recto por un plano paralelo a su directriz, actualmente es más común definir la parábola como un lugar geométrico: es la sección cónica resultante de cortar un cono recto con un plano cuyo ángulo de inclinación respecto al eje de revolución del cono sea igual al presentado por su generatriz. El plano resultará por lo tanto paralelo a dicha recta. Se define también como el lugar geométrico de los puntos de un plano que equidistan de una recta llamadadirectriz, y un punto exterior a ella llamado foco. En geometría proyectiva, la parábola se define como la curva envolvente de las rectas que unen pares de puntos homólogos en una proyectividadsemejante o semejanza.La parábola aparece en muchas ramas de las ciencias aplicadas debido a que su forma se corresponde con las gráficas de las ecuaciones cuadráticas. Por ejemplo, son parábolas las trayectorias ideales de los cuerpos que se mueven bajo la influencia exclusiva de la gravedad (ver movimiento parabólico y trayectoria balística).

De esta forma, una vez fija una recta y un punto se puede construir una parábola que los tenga por foco y directriz de acuerdo a la siguiente construcción. Sea T un punto cualquiera de la recta directriz. Se une con el foco dado F y a continuación se traza la mediatriz (o perpendicular por el punto medio) del segmento TF. La intersección de la mediatriz con la perpendicular por T a la directriz da como resultado un punto P que pertenece a la parábola. Repitiendo el proceso para diferentes puntos T se puede aproximar tantos puntos de la parábola como sea necesario.De la construcción anterior se puede probar que la parábola es simétrica respecto a la línea perpendicular a la directriz y que pasa por el foco. Al punto de intersección de la parábola con tal línea (conocida como eje de la parábola) se le conoce como vértice de la parábola y es el punto cuya distancia a la directriz es mínima. La distancia entre el vértice y el foco se conoce como distancia focal o radio focal.

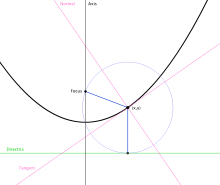
Lado rectoAl segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a la directriz, se le conoce como lado recto.Siendo D, E los extremos del lado recto y T, U las respectivas proyecciones sobre la directriz, denotando por W la proyección del foco F sobre la directriz, se observa que FEUW y DFWT son cuadrados, y sus lados miden FW=2FV. Por tanto el segmento DE es igual a 4 veces el segmento FV (la distancia focal).Las tangentes a la parábola que pasan por los extremos del lado recto forman ángulos de 45° con el mismo, consecuencia de que FEUW y DFWT sean cuadrados, junto con la construcción mencionada en la sección anterior. Además, tales tangentes se cortan en la directriz de forma perpendicular, precisamente en el punto de proyección W del foco, propiedades que pueden ser aprovechadas para construir una aproximación geométrica del foco y la directriz cuando éstos son desconocidos.

Semejanza de todas las parábolasDado que la parábola es una sección cónica, también puede describirse como la única sección cónica que tiene excentricidad  . La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.Desafortunadamente, al estudiar analíticamente las parábolas (basándose en ecuaciones), se suele afirmar erróneamente que los parámetros de la ecuación cambian la forma de la parábola, haciéndola más ancha o estrecha. La verdad es que todas las parábolas tienen la misma forma, pero la escala (zoom) crea la ilusión de que hay parábolas de formas diferentes.
. La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.Desafortunadamente, al estudiar analíticamente las parábolas (basándose en ecuaciones), se suele afirmar erróneamente que los parámetros de la ecuación cambian la forma de la parábola, haciéndola más ancha o estrecha. La verdad es que todas las parábolas tienen la misma forma, pero la escala (zoom) crea la ilusión de que hay parábolas de formas diferentes.
Un argumento geométrico informal es que al ser la directriz una recta infinita, al tomar cualquier punto y efectuar la construcción descrita arriba, se obtiene siempre la misma curva, salvo su escala, que depende de la distancia del punto a la directriz.

Tangentes a la parábolaUn resultado importante en relación a las tangentes de una parábola establece:Aplicaciones prácticasLlamemos F al foco de una parábola, P a un punto cualquiera de la misma y T a la proyección de este sobre la directriz. Sea MP la mediatriz del triángulo FPT, el cual es isósceles por ser iguales las distancias FP y PT, como se ha visto. Luego MP biseca al ángulo FPT, restando verificar si es tangente a la parábola en el punto P.Sea Q otro punto de la parábola y sea U su proyección en la directriz. Puesto que FQ=QU y QU<QT, entonces FQ<QT. Dado que esto es cierto para cualquier otro punto de la parábola, se concluye que toda la parábola está de un mismo lado de MP, y como la desigualdad es estricta, no hay otro punto de la parábola que toque a la recta MP, esto quiere decir que MP es la tangente de la parábola en P.
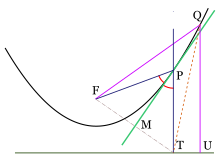
Una consecuencia de gran importancia es que la tangente refleja los rayos paralelos al eje de la parábola en dirección al foco. Las aplicaciones prácticas son muchas: las antenas satelitales yradiotelescopios aprovechan el principio concentrando señales recibidas desde un emisor lejano en un receptor colocado en la posición del foco.La concentración de la radiación solar en un punto, mediante un reflector parabólico tiene su aplicación en pequeñas cocinas solares y grandes centrales captadoras de energía solar.
Análogamente, una fuente emisora situada en el foco, enviará un haz de rayos paralelos al eje: diversas lámparas y faros tienen espejos con superficies parabólicas reflectantes para poder enviar haces de luz paralelos emanados de una fuente en posición focal. Los rayos convergen o divergen si el emisor se desplaza de la posición focal.


Ecuaciones de la parábolaCon el advenimiento de la geometría analítica se inició un estudio de las formas geométricas basado en ecuaciones y coordenadas.Una parábola cuyo vértice está en el origen y su eje coincide con el eje de las ordenadas, tiene una ecuación de la forma y=ax2 donde el parámetro a especifica la escala de la parábola, incorrectamente descrita como la forma de la parábola, ya que como se dijo antes, todas las parábolas tienen la misma forma. Cuando el parámetro es positivo, la parábola se abre «hacia arriba» y cuando es negativo se abre «hacia abajo».
Si bien, la expresión en forma de ecuación no fue posible hasta el desarrollo de la geometría analítica, la relación geométrica expresada en la ecuación anterior ya estaba presente en los trabajos de Apolonio,1 y se bosquejará a continuación usando notación moderna.
Tomando nuevamente la definición de parábola como sección de un cono recto de forma paralela a la directriz, sea V un punto en el eje y sea QV perpendicular al eje. (QV corresponde al valor x en la versión analítica y PV al valor y). Considerando la sección circular que pasa por Q y es paralela a la base del cono, obtenemos H, K paralelos a B y C.
Por el teorema de potencia de un punto:
 .
.
Al ser PM paralela a AC, los triángulos HVP, HKA y BCA son semejantes y así:
 .
.
Usando nuevamente los paralelismos:
 .
.
Despejando HV y VK para sustituir en la fórmula de QV² resulta en
 .
.
Pero el valor de  es una constante pues no depende de la posición de V, por lo que haciendo
es una constante pues no depende de la posición de V, por lo que haciendo

arroja la expresión moderna y=ax².
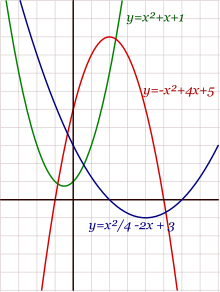
 Parábolas verticales, con ecuaciones de la forma y=ax²+bx+c.
Parábolas verticales, con ecuaciones de la forma y=ax²+bx+c.
Aplicando una sustitución de coordenadas podemos obtener ahora la ecuación de una parábola vertical para cualquier posición de su vértice.
La ecuación de una parábola cuyo eje es vertical y su vértice es (u,v) tiene la forma (y-v)=a(x-u)2,
agrupando los términos y reordenando se obtiene una forma equivalente:
La ecuación de una parábola cuyo eje es vertical es de la forma 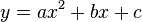 .
.
Si la parábola es horizontal, se obtienen ecuaciones similares pero intercambiando y por x y viceversa. Así tendríamos:
La ecuación de una parábola cuyo eje es horizontal es de la forma  .
.
Ecuación involucrando la distancia focal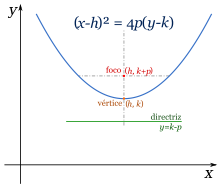
 Ecuación de una parábola vertical.
Ecuación de una parábola vertical.
Pueden haber muchas parábolas que tengan un mismo vértice (variando el parámetro a) en la primera ecuación. Sin embargo, dados dos puntos fijos, existe sólo una parábola que los tiene por vértice y foco ya que la directriz queda automáticamente fija como la perpendicular a la línea que une el foco con el vértice y a esa misma distancia del último.
Consideremos el caso especial en que el vértice es (0,0) y el foco es (0,p). La directriz es por tanto, la recta horizontal que pasa por (0,-p). A la distancia entre el vértice y el foco se le llama distancia focal, de modo que en este caso la distancia focal es igual a p. Con esta configuración se tiene:
La ecuación de una parábola con vértice en (0,0) y foco en (0,p) es  .
.
De forma alterna:
La ecuación de una parábola con vértice en (0,0) y foco en (0,p) es  .
.
Es de notar que el coeficiente 4p es precisamente la longitud del lado recto de la parábola.
Ambas ecuaciones se refieren a parábolas verticales que se abren «hacia arriba». La ecuación de una parábola que se abre hacia abajo es similar excepto que varía un signo. En este caso, el foco sería (0,-p) y de esta forma:
La ecuación de una parábola con vértice en (0,0) y foco en (0,-p) es  .
.
Cuando la parábola es horizontal «hacia la derecha», se obtiene una ecuación similar intercambiando los roles de x, y:
La ecuación de una parábola con vértice en (0,0) y foco en (p,0) es  ,
,
obteniendo mediante un cambio de signo la ecuación de las parábolas hacia la izquierda.
Finalmente, las ecuaciones cuando el vértice no está en el centro se obtienen mediante una traslación. En el caso común de la parábola vertical hacia arriba se tiene
La ecuación de una parábola con vértice en (h, k) y foco en (h, k+p) es  ,
,
mientras que para la parábola horizontal se intercambia x con y:.
La ecuación de una parábola con vértice en (h, k) y foco en (h+p, k) es 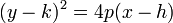 .
.
Ecuación general de una parábola.
La expresión algebraica que describe una parábola que ocupe cualquier posición en un plano es:

si y sólo si
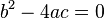
y los coeficientes a y c no pueden ser simultáneamente nulos
Hasta ahora se han descrito parábolas con sus ejes paralelos a alguno de los ejes de coordenadas. De esta forma las fórmulas son funciones de x ó de y. Pero una parábola puede tener su eje inclinado con respecto a un par de ejes de coordenadas ortogonales.
Mediante traslaciones y rotaciones es posible hallar un sistema de referencia en el que la ecuación anterior se exprese mediante una fórmula algebraica de la forma
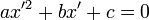 , donde a es distinto de cero.
, donde a es distinto de cero.
Elipse
Una elipse es la curva simétrica cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría –con ángulo mayor que el de la generatriz respecto del eje de revolución. Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado.

Elementos de una elipse.
La elipse es una curva plana y cerrada, simétrica respecto a dos ejes perpendiculares entre sí:
- El semieje mayor (el segmento C-a de la figura), y
- el semieje menor (el segmento C-b de la figura).
Miden la mitad del eje mayor y menor respectivamente.

Puntos de una elipse
Los focos de la elipse son dos puntos equidistantes del centro, F1 y F2 en el eje mayor. La suma de las distancias desde cualquier punto P de la elipse a los dos focos es constante, e igual a la longitud del diámetro mayor (d(P,F1)+d(P,F2)=2a).
Por comodidad denotaremos por PQ la la distancia entre dos puntos P y Q.
Si F1 y F2 son dos puntos de un plano, y 2a es una constante mayor que la distancia F1F2, un punto P pertenecerá a la elipse si se cumple la relación:

donde  es la medida del semieje mayor de la elipse.
es la medida del semieje mayor de la elipse.

Ejes de una elipse
El eje mayor, 2a, es la mayor distancia entre dos puntos opuestos de la elipse. El resultado de la suma de las distancias de cualquier punto a los focos es constante y equivale al eje mayor. El eje menor 2b, es la menor distancia entre dos puntos opuestos de la elipse. Los ejes de la elipse son perpendiculares entre sí.
Excentricidad de una elipse.
La excentricidad ε (épsilon) de una elipse es la razón entre su semidistancia focal (longitud del segmento que parte del centro de la elipse y acaba en uno de sus focos), denominada por la letra c, y su semieje mayor. Su valor se encuentra entre cero y
Modo de determinar los focos
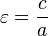 , con
, con 
Dado que 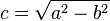 , también vale la relación:
, también vale la relación:
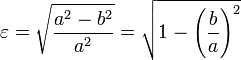
o el sistema:

La excentricidad indica la forma de una elipse; una elipse será más redondeada cuanto más se aproxime su excentricidad al valor cero. La designación tradicional de la excentricidad es la letra griega ε llamada épsilon.
(No se debe usar la letra e para designarla, porque se reserva para la base de los logaritmos naturales o neperianos. Véase: número e).
Constante de la elipse.
En la figura de la derecha se muestran los dos radio vectores correspondientes a cada punto P de una elipse, los vectores que van de los focos F1 y F2 a P. Las longitudes de los segmentos correspondientes a cada uno son PF1 (color azul) y PF2 (color rojo), y en la animación se ilustra como varían para diversos puntos P de la elipse.
Como establece la definición inicial de la elipse como lugar geométrico, para todos los puntos P de la elipse la suma de las longitudes de sus dos radio vectores es una cantidad constante igual a la longitud 2a del eje mayor:
- PF1 + PF2 = 2a
En la elipse de la imagen 2a vale 10 y se ilustra, para un conjunto selecto de puntos, cómo se cumple la definición.
Modo de determinar los focos.
El modo de determinar los focos a partir de los ejes, o un eje a partir de otro y los focos, se basa en la definición. Dibujados los dos ejes principales, se toma con el compás la medida a de la mitad del eje mayor. Haciendo centro en un extremo del eje menor, el compás cruza por el eje mayor en los focos.

Dado el eje mayor con los focos, la medida a aplicada a cada foco nos da arcos que se cruzan en los extremos del eje menor.
Dado un eje menor y la distancia de los focos, primero debemos hallar la recta sobre la que está el eje mayor, luego dibujar los focos a la distancia dada, y desde ellos tomar la distancia a los extremos del eje menor, que es la mitad del eje mayor.
Método de radios vectores
También denominado "por puntos"; con este método dibujamos un número suficiente de puntos mediante el compás. Como en el método tradicional visto antes usamos los radios vectores y la propiedad de que la suma de los radios vectores de un punto es igual a la medida del eje mayor.
Dados dos ejes principales y determinados los focos, se toman puntos al azar sobre el eje mayor entre el centro O y uno de los focos. Generalmente tres o cuatro, y preferiblemente cerca del foco por comodidad del dibujo.
Tomamos con el compás la distancia de un extremo del eje mayor (A) a cada uno de los puntos del eje (1). Haciendo centro en cada foco trazamos arcos con esa medida. A continuación tomamos el resto de la medida del eje mayor, desde el punto (1) al otro extremo (B), y con esa medida, haciendo centro de nuevo en los focos, cruzamos los arcos trazados antes. Las cruces nos dan puntos que pertenecen a la elipse.
Repitiendo la operación tantas veces como sea necesario obtenemos puntos de la elipse. Se completa el dibujo a mano o mediante plantillas de curvas.
Método de la tarjeta, compás de Arquímedes
Se puede dibujar la elipse mediante una regla de medir, un juego de escuadra y cartabón y un lápiz. Dibujamos los ejes principales con sus medidas, y determinamos los focos. Tomamos con la regla graduada, desde el 0, la distancia del centro al extremo del eje mayor, y después desde la marca del extremo del eje mayor, restamos la mitad del eje menor (ver dibujo). Apoyando el 0 de la regla en cualquier punto del eje menor y la diferencia calculada en el eje mayor, marcamos la medida del eje mayor. Para más claridad véase el dibujo.
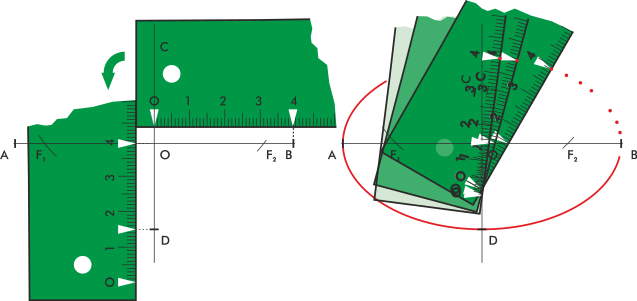 Esta misma operación se puede hacer con una tarjeta, y de ahí su nombre tradicional, haciendo marcas en el borde con las medidas dadas.
Para construirla con reglas y compás marcamos puntos arbitrarios en el eje menor. Tomando con el compás la medida de la mitad de la diferencia entre el eje mayor y el menor, hacemos centro en los puntos y señalamos puntos correspondientes en el eje mayor, a ambos lados. Dibujamos rectas desde los puntos del eje menor a sus correspondientes del eje mayor, prolongándolas. Sobre esas rectas, con el compás y desde cada punto del eje mayor, tomamos la medida de la mitad del eje menor, marcándola sobre la línea, lo que nos da los puntos de la elipse.
Existe una máquina sencilla (un elipsógrafo) hecha a base de guías o raíles y barras y llamada compás de Arquímedes, que se basa en este principio.
Esta misma operación se puede hacer con una tarjeta, y de ahí su nombre tradicional, haciendo marcas en el borde con las medidas dadas.
Para construirla con reglas y compás marcamos puntos arbitrarios en el eje menor. Tomando con el compás la medida de la mitad de la diferencia entre el eje mayor y el menor, hacemos centro en los puntos y señalamos puntos correspondientes en el eje mayor, a ambos lados. Dibujamos rectas desde los puntos del eje menor a sus correspondientes del eje mayor, prolongándolas. Sobre esas rectas, con el compás y desde cada punto del eje mayor, tomamos la medida de la mitad del eje menor, marcándola sobre la línea, lo que nos da los puntos de la elipse.
Existe una máquina sencilla (un elipsógrafo) hecha a base de guías o raíles y barras y llamada compás de Arquímedes, que se basa en este principio.
Construcción por afinidad.
Partimos de las rectas de los ejes principales. Se dibujan dos circunferencias concéntricas cuyos diámetros sean los de la elipse. Para hallar un punto trazamos un radio cualquiera de la circunferencia mayor fuera de los ejes. Desde el extremo del radio trazamos una recta auxiliar, paralela al eje menor, hacia dentro de la circunferencia. Desde el punto donde el radio corta la circunferencia menor trazamos una recta auxiliar paralela al eje mayor, que cruce la línea auxiliar que acabamos de hacer. El punto donde se cortan las dos auxiliares pertenece a la elipse.
Repitiendo la operación se obtienen todos los puntos que sean necesarios; la elipse se completa a mano o con plantillas. Normalmente por comodidad el dibujo se sistematiza; en lugar de los radios dibujamos diámetros completos, los trazos auxiliares verticales y horizontales se hacen de una vez mediante paralelas a los ejes.
 En este método se puede considerar una de las circunferencias como una doble transformación afín de la otra, y los puntos unidos por el mismo radio serían entonces afines. Una de las líneas auxiliares es la recta de afinidad de dos puntos (uno en la circunferencia, otro en la elipse), mientras la otra línea auxiliar da la reducción que corresponde
También se puede considerar la relación de las dos circunferencias una homología en la que el centro de homología coincide con el centro de una circunferencia, mientras su homóloga pertenece a un plano paralelo y también es concéntrica; estas homologías con rectas límite impropias son homotecias.
La ecuación de una elipse en coordenadas cartesianas, con centro en el origen, es:
En este método se puede considerar una de las circunferencias como una doble transformación afín de la otra, y los puntos unidos por el mismo radio serían entonces afines. Una de las líneas auxiliares es la recta de afinidad de dos puntos (uno en la circunferencia, otro en la elipse), mientras la otra línea auxiliar da la reducción que corresponde
También se puede considerar la relación de las dos circunferencias una homología en la que el centro de homología coincide con el centro de una circunferencia, mientras su homóloga pertenece a un plano paralelo y también es concéntrica; estas homologías con rectas límite impropias son homotecias.
La ecuación de una elipse en coordenadas cartesianas, con centro en el origen, es:
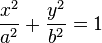
donde a > 0 y b > 0 son los semiejes de la elipse, donde si a corresponde al eje de las abscisas y b al eje de las ordenadas la elipse
es horizontal, si es al revés, entonces es vertical. El origen O es la mitad del segmento [FF']. La distancia entre los focos FF' se llama distancia focal y vale 2c = 2εa, siendo ε la excentricidad y a elsemieje mayor.
Forma cartesiana centrada fuera del origen.
Si el centro de la elipse se encuentra en el punto (h,k), la ecuación es:


Formas paramétricas
La ecuación paramétrica de una elipse con centro en  y siendo
y siendo  el semieje mayor y
el semieje mayor y  el menor, es:
el menor, es:

con  no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse, sino la anomalía excéntrica de la elipse. La relación entre
no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse, sino la anomalía excéntrica de la elipse. La relación entre  y θ es
y θ es
-
 .
.
La ecuación paramétrica de una elipse con centro en  en la que el parámetro
en la que el parámetro  sea concordante con el ángulo polar respecto al centro desplazado
sea concordante con el ángulo polar respecto al centro desplazado  es:
es:

con  . El parámetro
. El parámetro  es el ángulo de un sistema polar cuyo origen está centrado en
es el ángulo de un sistema polar cuyo origen está centrado en  .
.
Área interior de una elipse
El área de la superficie interior de una elipse es:

Siendo a y b los semiejes.
Perímetro de una elipse
El cálculo del perímetro de una elipse requiere del cálculo de integrales elípticas de segunda especie.
Sin embargo, el matemático Ramanujan dio una expresión sencilla que se aproxima razonablemente a la longitud de la elipse, pero en grado menor que la obtenida mediante integrales elípticas. Ramanujan, en su fórmula, utiliza el “semieje mayor” (a) y el “semieje menor” (b) de la elipse. Expresión aproximada del perímetro de una elipse:
![P \approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]\!\,](http://upload.wikimedia.org/math/4/5/3/4531867e543bc27be7c45f80a7599da1.png)
Propiedades notables
La elipse goza de ciertas propiedades asociadas a sus componentes, como se puede ver en Analogía de Michelson y Morley.
La elipse como cónica
La elipse surge de la intersección de una superficie cónica con un plano, de tal manera que la inclinación del plano no supere la inclinación de la recta generatriz del cono, consiguiendo así que la intersección sea una curva cerrada. En otro caso el corte podría ser una hipérbola o una parábola. Es por ello que a todas estas figuras bidimensionales se las llama secciones cónicas o simplemente cónicas.

La ecuación de una parábola cuyo eje es vertical y su vértice es (u,v) tiene la forma (y-v)=a(x-u)2,
La ecuación de una parábola cuyo eje es vertical es de la forma.
La ecuación de una parábola cuyo eje es horizontal es de la forma.
La ecuación de una parábola con vértice en (0,0) y foco en (0,p) es.
La ecuación de una parábola con vértice en (0,0) y foco en (0,p) es.
La ecuación de una parábola con vértice en (0,0) y foco en (0,-p) es.
La ecuación de una parábola con vértice en (0,0) y foco en (p,0) es,
La ecuación de una parábola con vértice en (h, k) y foco en (h, k+p) es,
La ecuación de una parábola con vértice en (h, k) y foco en (h+p, k) es.
Ecuación general de una parábola.
|
Hasta ahora se han descrito parábolas con sus ejes paralelos a alguno de los ejes de coordenadas. De esta forma las fórmulas son funciones de x ó de y. Pero una parábola puede tener su eje inclinado con respecto a un par de ejes de coordenadas ortogonales.
Mediante traslaciones y rotaciones es posible hallar un sistema de referencia en el que la ecuación anterior se exprese mediante una fórmula algebraica de la forma
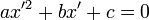 , donde a es distinto de cero.
, donde a es distinto de cero.Elipse
Una elipse es la curva simétrica cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría –con ángulo mayor que el de la generatriz respecto del eje de revolución. Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado.

Elementos de una elipse.
La elipse es una curva plana y cerrada, simétrica respecto a dos ejes perpendiculares entre sí:
- El semieje mayor (el segmento C-a de la figura), y
- el semieje menor (el segmento C-b de la figura).
Miden la mitad del eje mayor y menor respectivamente.

Puntos de una elipse
Los focos de la elipse son dos puntos equidistantes del centro, F1 y F2 en el eje mayor. La suma de las distancias desde cualquier punto P de la elipse a los dos focos es constante, e igual a la longitud del diámetro mayor (d(P,F1)+d(P,F2)=2a).
Por comodidad denotaremos por PQ la la distancia entre dos puntos P y Q.
Si F1 y F2 son dos puntos de un plano, y 2a es una constante mayor que la distancia F1F2, un punto P pertenecerá a la elipse si se cumple la relación:
donde  es la medida del semieje mayor de la elipse.
es la medida del semieje mayor de la elipse.
 es la medida del semieje mayor de la elipse.
es la medida del semieje mayor de la elipse.
Ejes de una elipse
El eje mayor, 2a, es la mayor distancia entre dos puntos opuestos de la elipse. El resultado de la suma de las distancias de cualquier punto a los focos es constante y equivale al eje mayor. El eje menor 2b, es la menor distancia entre dos puntos opuestos de la elipse. Los ejes de la elipse son perpendiculares entre sí.
Excentricidad de una elipse.
La excentricidad ε (épsilon) de una elipse es la razón entre su semidistancia focal (longitud del segmento que parte del centro de la elipse y acaba en uno de sus focos), denominada por la letra c, y su semieje mayor. Su valor se encuentra entre cero y
Modo de determinar los focos
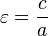 , con
, con 
Dado que 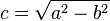 , también vale la relación:
, también vale la relación:
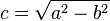 , también vale la relación:
, también vale la relación:
o el sistema:
La excentricidad indica la forma de una elipse; una elipse será más redondeada cuanto más se aproxime su excentricidad al valor cero. La designación tradicional de la excentricidad es la letra griega ε llamada épsilon.
(No se debe usar la letra e para designarla, porque se reserva para la base de los logaritmos naturales o neperianos. Véase: número e).
Constante de la elipse.
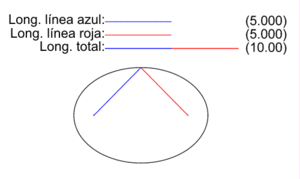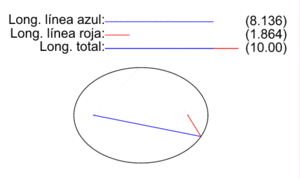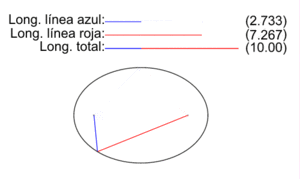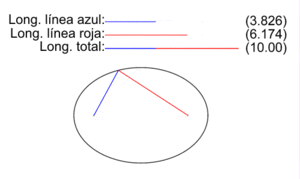
En la figura de la derecha se muestran los dos radio vectores correspondientes a cada punto P de una elipse, los vectores que van de los focos F1 y F2 a P. Las longitudes de los segmentos correspondientes a cada uno son PF1 (color azul) y PF2 (color rojo), y en la animación se ilustra como varían para diversos puntos P de la elipse.
Como establece la definición inicial de la elipse como lugar geométrico, para todos los puntos P de la elipse la suma de las longitudes de sus dos radio vectores es una cantidad constante igual a la longitud 2a del eje mayor:
- PF1 + PF2 = 2a
En la elipse de la imagen 2a vale 10 y se ilustra, para un conjunto selecto de puntos, cómo se cumple la definición.
Modo de determinar los focos.
El modo de determinar los focos a partir de los ejes, o un eje a partir de otro y los focos, se basa en la definición. Dibujados los dos ejes principales, se toma con el compás la medida a de la mitad del eje mayor. Haciendo centro en un extremo del eje menor, el compás cruza por el eje mayor en los focos.

Dado el eje mayor con los focos, la medida a aplicada a cada foco nos da arcos que se cruzan en los extremos del eje menor.
Dado un eje menor y la distancia de los focos, primero debemos hallar la recta sobre la que está el eje mayor, luego dibujar los focos a la distancia dada, y desde ellos tomar la distancia a los extremos del eje menor, que es la mitad del eje mayor.
Método de radios vectores
También denominado "por puntos"; con este método dibujamos un número suficiente de puntos mediante el compás. Como en el método tradicional visto antes usamos los radios vectores y la propiedad de que la suma de los radios vectores de un punto es igual a la medida del eje mayor.
Dados dos ejes principales y determinados los focos, se toman puntos al azar sobre el eje mayor entre el centro O y uno de los focos. Generalmente tres o cuatro, y preferiblemente cerca del foco por comodidad del dibujo.
Tomamos con el compás la distancia de un extremo del eje mayor (A) a cada uno de los puntos del eje (1). Haciendo centro en cada foco trazamos arcos con esa medida. A continuación tomamos el resto de la medida del eje mayor, desde el punto (1) al otro extremo (B), y con esa medida, haciendo centro de nuevo en los focos, cruzamos los arcos trazados antes. Las cruces nos dan puntos que pertenecen a la elipse.
Repitiendo la operación tantas veces como sea necesario obtenemos puntos de la elipse. Se completa el dibujo a mano o mediante plantillas de curvas.
Método de la tarjeta, compás de Arquímedes
Se puede dibujar la elipse mediante una regla de medir, un juego de escuadra y cartabón y un lápiz. Dibujamos los ejes principales con sus medidas, y determinamos los focos. Tomamos con la regla graduada, desde el 0, la distancia del centro al extremo del eje mayor, y después desde la marca del extremo del eje mayor, restamos la mitad del eje menor (ver dibujo). Apoyando el 0 de la regla en cualquier punto del eje menor y la diferencia calculada en el eje mayor, marcamos la medida del eje mayor. Para más claridad véase el dibujo.

Esta misma operación se puede hacer con una tarjeta, y de ahí su nombre tradicional, haciendo marcas en el borde con las medidas dadas.
Para construirla con reglas y compás marcamos puntos arbitrarios en el eje menor. Tomando con el compás la medida de la mitad de la diferencia entre el eje mayor y el menor, hacemos centro en los puntos y señalamos puntos correspondientes en el eje mayor, a ambos lados. Dibujamos rectas desde los puntos del eje menor a sus correspondientes del eje mayor, prolongándolas. Sobre esas rectas, con el compás y desde cada punto del eje mayor, tomamos la medida de la mitad del eje menor, marcándola sobre la línea, lo que nos da los puntos de la elipse.
Existe una máquina sencilla (un elipsógrafo) hecha a base de guías o raíles y barras y llamada compás de Arquímedes, que se basa en este principio.
Construcción por afinidad.
Partimos de las rectas de los ejes principales. Se dibujan dos circunferencias concéntricas cuyos diámetros sean los de la elipse. Para hallar un punto trazamos un radio cualquiera de la circunferencia mayor fuera de los ejes. Desde el extremo del radio trazamos una recta auxiliar, paralela al eje menor, hacia dentro de la circunferencia. Desde el punto donde el radio corta la circunferencia menor trazamos una recta auxiliar paralela al eje mayor, que cruce la línea auxiliar que acabamos de hacer. El punto donde se cortan las dos auxiliares pertenece a la elipse.
Repitiendo la operación se obtienen todos los puntos que sean necesarios; la elipse se completa a mano o con plantillas. Normalmente por comodidad el dibujo se sistematiza; en lugar de los radios dibujamos diámetros completos, los trazos auxiliares verticales y horizontales se hacen de una vez mediante paralelas a los ejes.

En este método se puede considerar una de las circunferencias como una doble transformación afín de la otra, y los puntos unidos por el mismo radio serían entonces afines. Una de las líneas auxiliares es la recta de afinidad de dos puntos (uno en la circunferencia, otro en la elipse), mientras la otra línea auxiliar da la reducción que corresponde
También se puede considerar la relación de las dos circunferencias una homología en la que el centro de homología coincide con el centro de una circunferencia, mientras su homóloga pertenece a un plano paralelo y también es concéntrica; estas homologías con rectas límite impropias son homotecias.
La ecuación de una elipse en coordenadas cartesianas, con centro en el origen, es:
donde a > 0 y b > 0 son los semiejes de la elipse, donde si a corresponde al eje de las abscisas y b al eje de las ordenadas la elipse
es horizontal, si es al revés, entonces es vertical. El origen O es la mitad del segmento [FF']. La distancia entre los focos FF' se llama distancia focal y vale 2c = 2εa, siendo ε la excentricidad y a elsemieje mayor.
Forma cartesiana centrada fuera del origen.
Si el centro de la elipse se encuentra en el punto (h,k), la ecuación es:

Formas paramétricas
La ecuación paramétrica de una elipse con centro en  y siendo
y siendo  el semieje mayor y
el semieje mayor y  el menor, es:
el menor, es:
 y siendo
y siendo  el semieje mayor y
el semieje mayor y  el menor, es:
el menor, es:
con  no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse, sino la anomalía excéntrica de la elipse. La relación entre
no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse, sino la anomalía excéntrica de la elipse. La relación entre  y θ es
y θ es
 no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse, sino la anomalía excéntrica de la elipse. La relación entre
no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse, sino la anomalía excéntrica de la elipse. La relación entre  y θ es
y θ es-
 .
.
La ecuación paramétrica de una elipse con centro en  en la que el parámetro
en la que el parámetro  sea concordante con el ángulo polar respecto al centro desplazado
sea concordante con el ángulo polar respecto al centro desplazado  es:
es:
 en la que el parámetro
en la que el parámetro  sea concordante con el ángulo polar respecto al centro desplazado
sea concordante con el ángulo polar respecto al centro desplazado  es:
es:
con  . El parámetro
. El parámetro  es el ángulo de un sistema polar cuyo origen está centrado en
es el ángulo de un sistema polar cuyo origen está centrado en  .
.
 . El parámetro
. El parámetro  es el ángulo de un sistema polar cuyo origen está centrado en
es el ángulo de un sistema polar cuyo origen está centrado en  .
.Área interior de una elipse
El área de la superficie interior de una elipse es:
Siendo a y b los semiejes.
Perímetro de una elipse
El cálculo del perímetro de una elipse requiere del cálculo de integrales elípticas de segunda especie.
Sin embargo, el matemático Ramanujan dio una expresión sencilla que se aproxima razonablemente a la longitud de la elipse, pero en grado menor que la obtenida mediante integrales elípticas. Ramanujan, en su fórmula, utiliza el “semieje mayor” (a) y el “semieje menor” (b) de la elipse. Expresión aproximada del perímetro de una elipse:
Propiedades notables
La elipse goza de ciertas propiedades asociadas a sus componentes, como se puede ver en Analogía de Michelson y Morley.
La elipse como cónica
La elipse surge de la intersección de una superficie cónica con un plano, de tal manera que la inclinación del plano no supere la inclinación de la recta generatriz del cono, consiguiendo así que la intersección sea una curva cerrada. En otro caso el corte podría ser una hipérbola o una parábola. Es por ello que a todas estas figuras bidimensionales se las llama secciones cónicas o simplemente cónicas.


No hay comentarios:
Publicar un comentario